Черчение и МХК

№ п\п	Т е м а	Количество учебных часов
1	ГРАФИЧЕСКОЕ ОБРАЗОВАНИЕ                  (4 ЧАСА)  Графическое образование, его назначение и место в общем образовании.	1 час
2 .	Графо – геометрические дисциплины, их назначение, отличительные особенности и возможности каждой в выстраивании образовательной траектории с учётом профессиональных интересов	1 час
3.	Пространственные представления. Пространственное и логическое мышление и его развитие средствами графических дисциплин.	1час
4.	ПРАКТИЧЕСКАЯ РАБОТА : Ознакомление с содержанием учебников различных графических дисциплин.	1 час
5.	КОММУНИКАТИВНЫЕ ВОЗМОЖНОСТИ ГРАФИЧКСКОГО ЯЗЫКА       (2 ЧАСА). Графический язык. Информация, передаваемая с помощью графического языка. Сферы деятельности, в которых графический язык является профессиональным языком общения.	1 час
6.	ПРАКТИЧЕСКАЯ РАБОТА: Выполнение задания на тему « Значение пространственных представлений в выбранной профессиональной деятельности»	1 час
7.	ГРАФИЧЕСКИЕ МЕТОДЫ НАУЧНОЙ, ПРОИЗВОДСТВЕННОЙ И ПРЕКТНО – КОНСТРУКТОРСКОЙ ДЕЯТЕЛЬНОСТИ              (24 ЧАСА). Проецирование. Центральное проецирование ( перспектива ).	1 час
8.	Использование перспективных изображений в проектной деятельности.	1 час
9.	Параллельное проецирование. Ортогональное и косоугольное проецирование.	1 час
10.	Параллельное проецирование на две и три взаимно перпендикулярные плоскости проекции. Особенности использования метода в проектной деятельности.	1 час
11.	Аксонометрические проекции.	1 час
12.	Стандартные Аксонометрические проекции ( прямоугольная изометрическая проекция, косоугольная горизонтальная диметрическая проекция )	1 час
13.	Наброски, поисковые , технические рисунки и их назначение в пректной работе.	1 час
14.	Приёмы выполнения технического рисунка.	1 час
15.	ГРАФИЧЕСКАЯ РАБОТА №1: «Выполнение аксонометрической проекции несложного изделия, используемого в предполагаемой сфере профессиональных интересов школьника».	2 часа
16.	Чертёж, как основной документ.	1 час
17.	Оформление проектной документации (шрифты, форматы, основная надпись, масштабы изображения)	1 час
18.	ГРАФИЧЕСКАЯ РАБОТА №2: « Выполнение чертежа трёхмерного объекта, используемого в профессиональной деятельности интересов школьника».	2 часа
19.	Особенности нанесения размеров в архитектурных, строительных, дизайнерских и технических проектах.	2 час
20.	Плавные переходы поверхностей и их отображение в проектной документации.	1 час
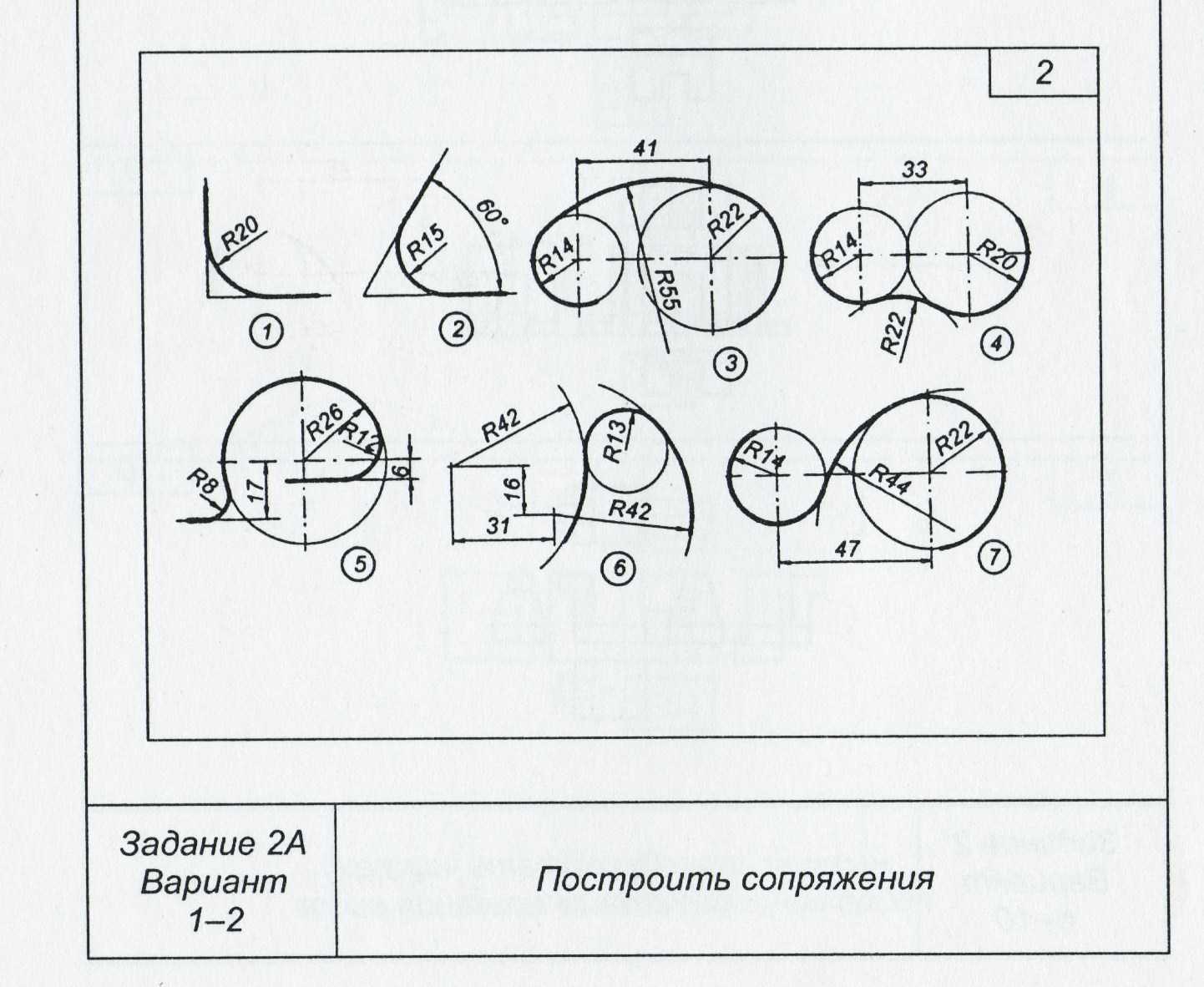
21.	Сопряжение на чертежах и аксонометрических проекциях.	1 час
22.	Чертежи деталей и сборочных единиц. Изображения на сборочных чертежах ( виды, разрезы, сечения).	1 час
23.	Условности и упрощения. Правила нанесения размеров на сборочных чертежах	1 час
24.	Техническая и технологическая информация на сборочных чертежах.	1 час
25.	Конструирование недостающих деталей сборочных единиц по заданным условиям.	1 час
26.	Выполнение сборочных чертежей. Чтение сборочных чертежей. Деталирование.	1 час
27.	ГРАФИЧЕСКАЯ РАБОТА №3: «Выполнение сборочного чертежа, состоящего из 3-х деталей».	1 час
28.	ГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ И ИХ ИСПОЛЬЗОВАНИЕ В РАЗЛИЧНЫХ СФЕРАХ ЖИЗНИ И ДЕЯТЕЛЬНОСТИ                         ( 2 ЧАСА) Графические изображения в быту, науке и технике, архитектуре и строительстве, дизайне, изобразительном искусстве. Графические изображения, используемые в проектных чертежах : виды, фасады, сечения, разрезы, планы, выносной элемент. Особенности изображений на архитектурных, архитектурно-строительных, инженерно строительных и  технических чертежах.	1 час
29.	ВЫПОЛНЕНИЕ РЕФЕРАТА  на одну из заданных тем: « Использование графических изображений в различных сферах жизни и деятельности», « Графические изображения в области моих профессиональных интересов»	2 часа
30.	ПЕРСПЕКТИВНЫЕ ИЗМЕНЕНИЯ В ГРАФИЧЕСКОМ ОТОБРАЖЕНИИ ИНФОРМАЦИИ            ( 2 ЧАСА). Компьютеризация процессов создания конструкторской документации.	1 час
31.	Пересмотр стандартов ЕСКД с целью сокращения, упрощения его требований в соответствии с особенностями компьютерной графики. Расширение знаковой системы в связи с появлением новых материалов и технологий изготовления изделий.	1 час
32.	СРЕДСТВА СОЗДАНИЯ ГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ        (2 ЧАСА). Технические и традиционные средства создания (выполнения) графических изображений.	2 часа
		ИТОГО : 36 часов

 

 Возможно информация, находящаяся здесь поможет Вам при изучении таких предметов как "Черчение" (элективный курс) и Мировая Художественная Культура. На этом блоге будут вывешиваться домашние задания; дополнительный материал, который отсутствует в учебнике.

ВВЕДЕНИЕ

1. Содержание и задачи курса начертательной геометрии.

Трудно указать такой вид человеческой деятельности, где, решая ту или иную техническую или нетехническую задачу, не приходилось бы прибегать к помощи изображений машин и механизмов, планов строений и т.п.

К. Маркс указывал, что всякий процесс труда человека заканчивается результатом, который уже в начале этого процесса имелся в его представлении: "Паук совершает операции, напоминающие операции ткача, и пчела постройкой своих восковых ячеек посрамляет некоторых людей - архитекторов. Но самый плохой архитектор от наилучшей пчелы с самого начала отличается тем, что, прежде чем строить ячейку из воска, он уже построил её в своей голове".

Сколь широка и многогранна деятельность человека, столь и различны требования, предъявляемые к форме и содержанию изображений. Одни из них должны производить на глаз человека такое же впечатление, какое производит и сам изображаемый предмет, иначе говоря, изображение должно обладать достаточной наглядностью. В другом случае изображение должно быть, в первую очередь, геометрически равноценно оригиналу, оно должно давать полную геометрическую и размерную характеристику изображаемого предмета. Этому требованию должен отвечать, например, всякий машиностроительный чертёж.

Наконец, к изображению могут быть предъявлены оба указанных условия одновременно - наглядность изображения должна сочетаться с геометрической равноценностью оригиналу.

Изображения различных предметов и объектов не являются самоцелью, они дают возможность решать инженеру по ним различные технические задачи.

Однако не всякое изображение может быть использовано для решения технических задач. Для этого оно, в первую очередь, должно быть геометрически равноценно изображаемому объекту, то есть, построено по определённому геометрическому закону. Вопросами исследования геометрических основ построения изображений предметов на плоскости, вопросами решения пространственных геометрических задач при помощи изображений занимается одна из ветвей геометрии - НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.

Начертательная геометрия относится к числу математических наук. Для неё характерна та общность методов, которая свойственна каждой математической науке. Методы начертательной геометрии находят самое широкое применение в объектах изучения самой различной природы: в механике, архитектуре и строительстве, химии, геодезии, геологии, кристаллографии и т.д.

Но наибольшее значение и применение методы начертательной геометрии нашли в различных областях техники при составлении различного вида технических чертежей: машиностроительных, строительных, различного рода карт и т.д. Начертательная геометрия, таким образом, является звеном, соединяющим математические науки с техническими.

Начертательная геометрия входит в группу общетехнических дисциплин, составляющих основу всякого инженерного образования. Она учит грамотно владеть выразительным техническим языком - языком чертежа, умению составлять и свободно читать чертежи, решать при помощи чертежей различные инженерно-технические задачи.

Кроме того, изучение начертательной геометрии способствует развитию у студентов пространственных представлений и пространственного воображения - качеств, характеризующих высокий уровень инженерного мышления и необходимых для решения прикладных задач.

В процессе изучения начертательной геометрии достигаются и другие цели, расширяется общенаучный кругозор студентов, развиваются навыки логического мышления, внимательность, наблюдательность, аккуратность и другие качества, развитие которых является одной из задач обучения и воспитания в высшей технической школе.

Предметом начертательной геометрии (в узком смысле) является изучение теории построения плоских моделей пространств и теории и практики решения пространственных задач на таких плоских моделях.

Цели курса:

1. Научить пространственно мыслить и отображать на плоскости трёхмерные геометрические образы (фигуры).
2. Развить способность мысленного восприятия пространственного геометрического образа по его отображению на плоскости, т.е. научить читать чертёж.
   (Таким образом, мы решаем две задачи: прямую и обратную. Объёмный предмет отображаем на плоскости - прямая задача. По плоскому чертежу представляем объёмную форму предмета - обратная задача. Прочесть чертёж - это представить себе пространственное изображение предмета.)
3. Сообщить знания о методах решения на плоскости пространственных метрических и позиционных задач.

 

2. Роль русских и советских учёных в разработке и развитии методов изображений.

Сведения и приёмы построений, обуславливаемые потребностью в плоских изображениях пространственных форм, накапливались постепенно с древних времён. В течение продолжительного периода плоские изображения выполнялись как изображения наглядные. С развитием техники первостепенное значение приобрёл вопрос о применении метода, обеспечивающего точность и удобоизмеримость изображений, т.е. возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путём простых приёмов определить размеры отрезков линий и фигур. Постепенно накопившиеся отдельные правила и приёмы построения таких изображений были приведены в систему и развиты в труде французского учёного Монжа, изданном в 1799 году. Изложенный Гаспаром Монжем (1746-1818) метод - метод ортогонального проецирования - обеспечивал выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остаётся основным методом составления технических чертежей.

Чертёж - язык инженера, начертательная геометрия - грамматика этого языка.

В нашей стране начертательную геометрию начали преподавать с 1810 года в ЛИЖТе - первом ВУЗе страны, только что организованном. Лекции там читал Я.А. Севастьянов (1796-1849), с именем которого связано появление первого оригинального труда под названием "Основания начертательной геометрии" (1821 г.), в основном посвящённого изложению метода Монжа.

Крупный след в развитии начертательной геометрии в России в XIX веке оставили Н.И. Макаров (1824-1904) (адмирал Макаров, погибший в Порт-Артуре) и В.И. Курдюнов (1853-1904).

Если начертательная геометрия как предмет возникла из нужд практики и в середине XIX века она расширила свои разделы, то к началу XX века аналитические методы, применённые в начертательной геометрии, вышли на первый план, точность графических методов не удовлетворялась и начертательная геометрия пошла на убыль. Последними книгами были книги Н.А. Рышина (1877-1942) и В.О. Гордона.

С появлением трудов Н.Ф. Четверухина (1891-1973) начертательная геометрия была выведена из застоя. Н.Ф. Четверухин стал рассматривать начертательную геометрию как самостоятельную науку (не связанную с черчением). Он первый увидел, что методами начертательной геометрии можно решать сложные конструктивные задачи. Появилась "Прикладная геометрия" и начался её расцвет. За период с конца 40-х годов начертательная геометрия развивалась и расширялась. В науке большая роль принадлежит И.И. Котову (1905-1975) и его ученикам. После смерти Н.Ф. Четверухина начался процесс сокращения часов по начертательной геометрии и произошел застой. В 1982 г. вопрос в ВАКе был решён положительно и предмет восстановлен.

Центральное проецирование.

Центральное проецирование - наиболее общий случай получения проекций геометрических фигур. Сущность его состоит в следующем:

 (Читать дальше...)

                                    Сопряжение. 

 Сопряжение- плавный переход одной линии в другую.

    

                        Сопряжение пересекающихся прямых дугой окружности заданного радиуса.

           Задача сводится к проведению окружности, касающейся обеих заданных прямых линий.

 

   Вариант 1.

 

  Проводим вспомогательные прямые параллельно заданным на расстоянии  R от заданных.

  Точка пересечения этих прямых будет центром О дуги сопряжения. Перпендикуляры, опущенные из центра О на       

  заданные прямые, определят точки касания К и К₁.

 

                                                   

                                                   Сопряжения. Построение сопряжения линий.

 

   Вариант 2.

 

  Построение такое же.

 

                                           

                                           Сопряжения. Построение сопряжения линий.

 

   Вариант 3.

 

  Если требуется провести окружность, чтобы она касалась трех пересекающихся прямых линий, то в этом случае

 радиус не может быть задан условиями задачи. Центр О окружности находится на пересечении биссектрис углов

 В и С. Радиусом окружности является перпендикуляр, опущенный из центра О на любую из 3-х заданных прямых

 линий.

 

                                                  

                                                  Сопряжения. Построение сопряжений линий.

 

          Построение внешнего сопряжения данной окружности с данной прямой дугой заданного радиуса R₁.

 

  Из центра О данной окружности проводим дугу вспомогательной окружности радиусом R+R₁.

  Проводим прямую параллельно заданной на расстоянии R₁.

  Пересечение прямой и  вспомогательной дуги даст точку центра дуги сопряжения О₁.

  Точка касания дуг К лежит на линии ОО₁.

  Точка касания дуги и линии К₁ лежит на пересечении перпендикуляра из точки О₁ на прямую с дугой.

 

                                             

                                             Сопряжения. Построение внешнего сопряжения окружности с прямой.

 

   Построение внутреннего сопряжения данной окружности с  данной прямой дугой заданного радиуса R₁.

 

  Из центра О данной окружности проводим  вспомогательную окружность радиусом R- R₁.

  Дальше см. предыдущие построения.

 

 

                                              

                                              Сопряжения. Построение внутреннего сопряжения окружности с прямой.

 

          Построение сопряжения двух данных окружностей дугой заданного радиуса R₃.

 

  Внешнее касание.

 

  Из центра окружности О₁ описываем дугу вспомогательной окружности радиусом R₁+R₃.

  Из центра окружности О₂ описываем дугу вспомогательной окружности радиусом R₂+R₃.

  Пересечение дуг вспомогательных окружностей даст точку О₃, которая является центром дуги сопряжения

  (окружности с радиусом R₃).

  Точки касания К₁ и К₂ находятся на линиях О₁О₃ и О₂О₃.

 

                                              

                                              Сопряжения. Сопряжение двух окружностей дугой.

 

  Внутреннее касание

 

  Из центра окружности О₁ описываем дугу вспомогательной окружности радиусом R₃-R₁.

  Из центра окружности О₂ описываем дугу вспомогательной окружности радиусом R₃- R₂.

  Пересечение дуг вспомогательных окружностей даст точку, которая является центром дуги сопряжения

  (окружности с радиусом R₃).

 

                            

                            Сопряжения. Сопряжение двух окружностей дугой.

 

  Внешнее и внутреннее касание.

  Заданы две окружности с центрами О₁ и О₂ с радиусами r₁ и r₂. Необходимо провести окружность заданного

  радиуса R так, чтобы обеспечить с одной окружностью внутреннее касание, а с другой - внешнее.

 

  Из центра окружности О₁ описываем дугу вспомогательной окружности радиусом R-r₁.

  Из центра окружности О₂ описываем дугу вспомогательной окружности радиусом R+r₂.

  Пересечение дуг вспомогательных окружностей даст точку, которая является центром дуги сопряжения

  (окружности с радиусом R).

 

                                          

                                          Сопряжения. Сопряжение двух окружностей дугой.

 

          Построение окружности, проходящей через заданную точку А и касающейся данной окружности

          в заданной точке В.

 

  Находим середину прямой линии АВ. Через середину линии АВ поводим перпендикуляр. Пересечение продолжения

  линии ОВ и перпендикуляра дает точку О₁. О₁ - центр искомой окружности с радиусом R = O₁B = O₁A.

 

                                               

                                               Сопряжения. Внутреннее касание окружности и дуги.

 

          Построение сопряжения окружности с прямой линией в заданной на прямой точке А.

 

  Из заданной точки А линии LM восстанавливаем перпендикуляр к прямой линии LM. На продолжении

  перпендикуляра откладываем отрезок АВ. АВ = R. Соединяем точку В с центром окружности О₁ прямой.

  Из точки А проводим прямую линию параллельно ВО₁ до пересечения с окружностью. Получим точку К - точку

  касания. Соединим точку К с центром окружности О₁. Продлим линии О₁К и АВ до пересечения. Получим точку

  О₂, которая является центром дуги сопряжения с радиусом О₂А = О₂К.

 

                                        

                                        Сопряжения. Сопряжение окружности с прямой в заданной точке.

 

          Построение сопряжения окружности с прямой линией в заданной на окружности точке А.

 

  Внешнее касание.

  Проводим касательную к окружности через точку А. Пересечение касательной с прямой линией LM даст точку В.

  Делим угол, образованный касательной и прямой линией LM, пополам. Пересечение биссектрисы угла и

  продолжения радиуса ОА даст точку О₁. О₁ - центр дуги сопряжения с радиусом О₁А = О₁К.

 

 

                                               

                                               Сопряжения. Сопряжение окружности с прямой в заданной точке на окружности.

 

   Внутреннее касание.

  Проводим касательную к окружности через точку А. Пересечение касательной с прямой LM даст точку В.

  Делим угол, образованный касательной и прямой линией LM, пополам. Пересечение биссектрисы угла и

  продолжения радиуса ОА даст точку О₁. О₁ - центр дуги сопряжения с радиусом О₁А = О₁К.

 

                                               

                                               Сопряжения. Сопряжение окружности  с прямой в заданной точке на окружности.

 

          Построение сопряжения двух неконцентрических дуг окружностей дугой заданного радиуса.

 

   Проводим из центра дуги О₁ вспомогательную дугу радиусом R₁-R₃. Проводим из центра дуги О₂ вспомогательную

  дугу радиусом R₂+R₃. Пересечение дуг даст точку О. О - центр дуги сопряжения с радиусом R₃. Точки касания

  К₁ и К₂ лежат на линиях ОО₁ и ОО₂.

 

                                               

                                               Сопряжения. Сопряжение 2-х неконцентрических дуг окружностей дугой.

 

          Построение лекальной кривой подбором дуг.

 

  Подбирая  центры дуг, совпадающих с участками кривой, можно циркулем вычертить любую лекальную кривую.

  Для того чтобы дуги плавно переходили одна в другую, необходимо, чтобы точки их сопряжения (касания)

  находились на прямых линиях, соединяющих центры этих дуг.

  Последовательность построений.

  Подбираем центр 1 дуги произвольного участка ab.

  На продолжении первого радиуса подбираем центр 2 радиуса  дуги участка bc.

  На продолжении второго радиуса подбираем центр 3 радиуса  дуги участка cd и т. д.

  Так строим всю кривую.

 

 

                                               

                                               Сопряжения. Подбор дуг.

 

          Построение сопряжения двух параллельных прямых двумя дугами.

 

  Заданные на прямых параллельных линиях точки А и В соединяем линией АВ.

  Выбираем на прямой АВ произвольную точку М.

  Делим отрезки АМ и ВМ пополам.

  Восстанавливаем в серединах отрезков перпендикуляры.

  В точках А и В, заданных прямых, восстанавливаем перпендикуляры к прямым.

 

  Пересечение соответствующих перпендикуляров даст точки О₁ и О₂.

  О₁ центр дуги сопряжения с радиусом О₁А = О₁М.

  О₂ центр дуги сопряжения с радиусом О₂В = О₂М.

  Если точку М выбрать на середине линии АВ, то радиусы дуг сопряжения будут равны.

  Касание дуг в точке М, находящейся на линии О₁О₂.

 

                                              

                                              Сопряжения. Сопряжение параллельных прямых двумя дугами.

Проецирование точки на три плоскости проекций.

Чтобы получить эпюр точки, нужно преобразовать пространственный макет.
Фронтальная проекция точки А - A₂ остаётся на месте, как принадлежащая плоскости V, которая не меняет своего положения.
Горизонтальная проекция A₁ вместе с горизонтальной плоскостью проекций H, совмещаемой с плоскостью чертежа, опустится вниз и расположится на одном перпендикуляре к оси x с фронтальной проекцией A₂.
Профильная проекция A₃ будет вращаться вправо вместе с профильной плоскостью проекций W до совмещения с плоскостью чертежа. При этом A₃ будет принадлежать перпендикуляру к оси z, проведённому через A₂, и удалена от оси z на такое же расстояние, на которое горизонтальная проекция A₁ удалена от оси x.

Таким образом, ЭПЮРОМ (комплексным чертежом точки) называется плоское изображение, полученное в результате ортогонального проецирования на две или несколько взаимно перпендикулярных плоскостей путём последующего совмещения этих плоскостей с одной плоскостью проекций (рис.7).

Рис.7

Биссектрису угла между осями y называют постоянной прямой Ко эпюра Монжа. Полученная модель (эпюр) несёт такую же информацию, какая содержится в пространственном макете.

Действительно, чтобы определить положение точки А в пространстве, необходимо знать 3 её координаты (x,y,z) - длины отрезков [AA₃],[AA₂],[AA₁]. Величины этих отрезков могут быть определены на эпюре.
[AA₃]=[A₁A_y]=[A₂A_z]
[AA₂]=[A₁A_x]=[A₃A_z]
[AA₁]=[A₂A_x]=[A₃A_y]

Горизонтальная проекция точки А определяется абсциссой x и ординатой y, фронтальная - x и z, профильная - y и z, т.е.
A₁(x,y)
A₂(x,z)
A₃(y,z)

Отсюда следует, в частности, что:

1. 1.     положение точки в пространстве вполне определяется положением её двух ортогональных проекций (т.к. по двум любым заданным ортогональным проекциям точки всегда можно построить недостающую её третью ортогональную проекцию)
2. 2.     горизонтальная и фронтальная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси x
   горизонтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси y
   фронтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси z

 

Эпюр Монжа. Постепенно накопившиеся отдельные правила и приемы построения изображений и решения задач были обобщены и сведены воедино французским ученым-геометром Гаспаром Монжем с своем классическом труде «Geometrie descriptive» («Начертательная геометрия»), опубликованном в 1799 году. Он разработал общую теорию построения ортогональных проекций трехмерного типа на плоском листе, известную под названием эпюр Монжа (Epure – от франц. чертеж, проект). Условно можно разделить метод на систему двух и трех плоскостей проекций.

 

	Система двух плоскостей проекций В данном случае, для построения изображения в двух плоскостях проекций, горизонтальная плоскость проекций П1 и фронтальная плоскость проекций П2 совмещаются в одну, как показано на рис.1. В пересечении они дают ось проекций x и делят пространство на четыре четверти (квадранта). Рис.1. Система двух плоскостей проекций: а – расположение плоскостей проекций; б – совмещение плоскостей проекций

 

	Система трех плоскостей проекций В системе трех плоскостей проекций совмещаются все три плоскости проекций (П1 – горизонтальная, П2 – фронтальная и П3 – профильная), как показано на рис.2. Плоскости образуют три оси проекций (оси координат) и восемь прямоугольных трехгранников, деля пространство на восемь октантов. Для проецирования точки А на плоскости проекций используются следующие ее координаты: П1 – А′(x, y) П2 – А′′(x, z) П3 – А′′′(y, z) Рис.2. Система трех плоскостей проекций: а – расположение плоскостей проекций; б – совмещение плоскостей проекций